Please use left and right arrows to navigate. On a smartphone, you can just scroll.

Unbalanced Optimal Transport:
A Unified Framework for Object Detection

CVPR 2023 - Poster: TUE-AM-304

  • Henri De Plaen
    1*
  • Pierre-François De Plaen
    2*
  • Johan A. K. Suykens
    1
  • Marc Proesmans
    2
  • Tinne Tuytelaars
    2
  • Luc Van Gool
    2,3
  • 1
    ESAT-STADIUS, KU Leuven, Belgium
  • 2
    ESAT-PSI, KU Leuven, Belgium
  • 3
    Computer Vision Lab, ETH Zürich, Switzerland

Training

1 Output \(N_p\) predictions

Model
  • \(\hat{b}^{(1)}\), \(\hat{c}^{(1)}\)
  • \(\hat{b}^{(2)}\), \(\hat{c}^{(2)}\)
  • \(\vdots\)
  • \(\hat{b}^{(5)}\), \(\hat{c}^{(5)}\)
1
2
3
4
5

2 Assign predictions to GT boxes

1
2
3
4
5
A
B
  • 1
  • 2
  • 3
  • 4
  • 5
  • A
  • B
GIoU
cost matrix

3 Loss: improve assigned, discard others

Matching Strategies

1
2
3
4
5
A
B
  • 1
  • 2
  • 3
  • 4
  • 5
  • A
  • B
  • \(\varnothing\)
GIoU cost matrix

Pred. to best GT

  • 1
  • 2
  • 3
  • 4
  • 5
100
001
001
100
010
  • A
  • B
  • \(\varnothing\)
  • 1
  • 2
  • 3
  • 4
  • 5
10
01
10
10
01
  • A
  • B
  • 1
  • 2
  • 3
  • 4
  • 5
  • A
  • B
  • \(\varnothing\)

GT to best pred.

  • 1
  • 2
  • 3
  • 4
  • 5
001
001
001
110
001
  • A
  • B
  • \(\varnothing\)
  • 1
  • 2
  • 3
  • 4
  • 5
  • A
  • B
  • \(\varnothing\)

Hungarian Matching

  • 1
  • 2
  • 3
  • 4
  • 5
001
001
001
100
010
  • A
  • B
  • \(\varnothing\)
  • 1
  • 2
  • 3
  • 4
  • 5
  • A
  • B
  • \(\varnothing\)

A Unifying Framework

1
2
3
4
5
A
B
  • 1
  • 2
  • 3
  • 4
  • 5
  • A
  • B
  • \(\varnothing\)
  • \(\varnothing\)
  • \(\varnothing\)
GIoU cost matrix

DEtection TRansformer (DETR)

  • 1
  • 2
  • 3
  • 4
  • 5
01000
00100
00010
10000
00001
  • A
  • B
  • \(\varnothing\)
  • \(\varnothing\)
  • \(\varnothing\)
$$ \begin{aligned} \min_{\sigma \in \text{Perm}(N_p)} & \frac{1}{n} \sum_{i=1}^{N_p} C_{i,\sigma(i)} \end{aligned} $$
$$ \begin{aligned} \min_{\mathbf{P} \in \{0,1\}^{N_p \times N_g} } & < \mathbf{P},\mathbf{C} > \\ s.t. & \sum_{j} P_{ij} = 1 \quad \forall i \\ & \sum_{i} P_{ij} = 1 \quad \forall j \end{aligned} $$

Optimal Transport Leonid Kantorovich (Nobel Prize 1975)

  • 1
  • 2
  • 3
  • 4
  • 5
  • A
  • B
  • \(\varnothing\)
  • 1
  • 2
  • 3
  • 4
  • 5
01000
000.330.330.33
000.330.330.33
10000
000.330.330.33
  • A
  • B
  • \(\varnothing\)
  • \(\varnothing\)
  • \(\varnothing\)
$$ \begin{aligned} \min_{\mathbf{P} \in \mathbb{R}_{+}^{N_p \times N_g} } < \mathbf{P},\mathbf{C} > & - \epsilon \mathbf{H}(\mathbf{P}) \\ & + \textcolor{red}{10^{-3}} \mathrm{KL}\left(\boldsymbol{P} \mathbf{1}_{N_g} \| \boldsymbol{\alpha}\right) \\ & + \textcolor{red}{10^{3}} \mathrm{KL}\left(\mathbf{1}_{N_p}^{\top} \boldsymbol{P} \| \boldsymbol{\beta}\right) \\ \end{aligned} $$
$$ \begin{aligned} \min_{\mathbf{P} \in \mathbb{R}_{+}^{N_p \times N_g} } < \mathbf{P},\mathbf{C} > & - \epsilon \mathbf{H}(\mathbf{P}) \\ & + \textcolor{red}{10^{3}} \mathrm{KL}\left(\boldsymbol{P} \mathbf{1}_{N_g} \| \boldsymbol{\alpha}\right) \\ & + \textcolor{red}{10^{-3}} \mathrm{KL}\left(\mathbf{1}_{N_p}^{\top} \boldsymbol{P} \| \boldsymbol{\beta}\right) \\ \end{aligned} $$
$$ \begin{aligned} \min_{\mathbf{P} \in \mathbb{R}_{+}^{N_p \times N_g} } < \mathbf{P},\mathbf{C} > & - \epsilon \mathbf{H}(\mathbf{P}) \\ & + \tau_1 \mathrm{KL}\left(\boldsymbol{P} \mathbf{1}_{N_g} \| \boldsymbol{\alpha}\right) \\ & + \tau_2 \mathrm{KL}\left(\mathbf{1}_{N_p}^{\top} \boldsymbol{P} \| \boldsymbol{\beta}\right) \\ \end{aligned} $$
$$ \begin{aligned} \min_{\mathbf{P} \in \mathbb{R}_{+}^{N_p \times N_g} } & < \mathbf{P},\mathbf{C} > \textcolor{red}{- \epsilon \mathbf{H}(\mathbf{P})} \\ s.t. & \sum_{j} P_{ij} = \alpha_i \quad \forall i \\ & \sum_{i} P_{ij} = \beta_j \quad \forall j \end{aligned} $$ \( \textcolor{red}{\mathbf{H}(\mathbf{P}) \stackrel{} = -\sum_{i, j} \mathbf{P}_{i, j}\left(\log \left(\mathbf{P}_{i, j}\right)-1\right)} \)
$$ \begin{aligned} \min_{\mathbf{P} \in \mathbb{R}_{+}^{N_p \times N_g}} & < \mathbf{P},\mathbf{C} > \\ s.t. & \sum_{j} P_{ij} = \textcolor{red}{\alpha_i} \quad \forall i \\ & \sum_{i} P_{ij} = \textcolor{red}{\beta_j} \quad \forall j \end{aligned} $$
$$ \begin{aligned} \min_{\mathbf{P} \in \textcolor{red}{\mathbb{R}_{+}^{N_p \times N_g}} } & < \mathbf{P},\mathbf{C} > \\ s.t. & \sum_{j} P_{ij} = 1 \quad \forall i \\ & \sum_{i} P_{ij} = 1 \quad \forall j \end{aligned} $$

Entropic Regularization: Motivation

1
2
A
  • 1
  • 2
  • A
  • \(\varnothing\)
GIoU cost matrix

Hungarian Matching

  • 1
  • 2
  • A
  • \(\varnothing\)

Optimal Transport

  • 1
  • 2
  • A
  • \(\varnothing\)

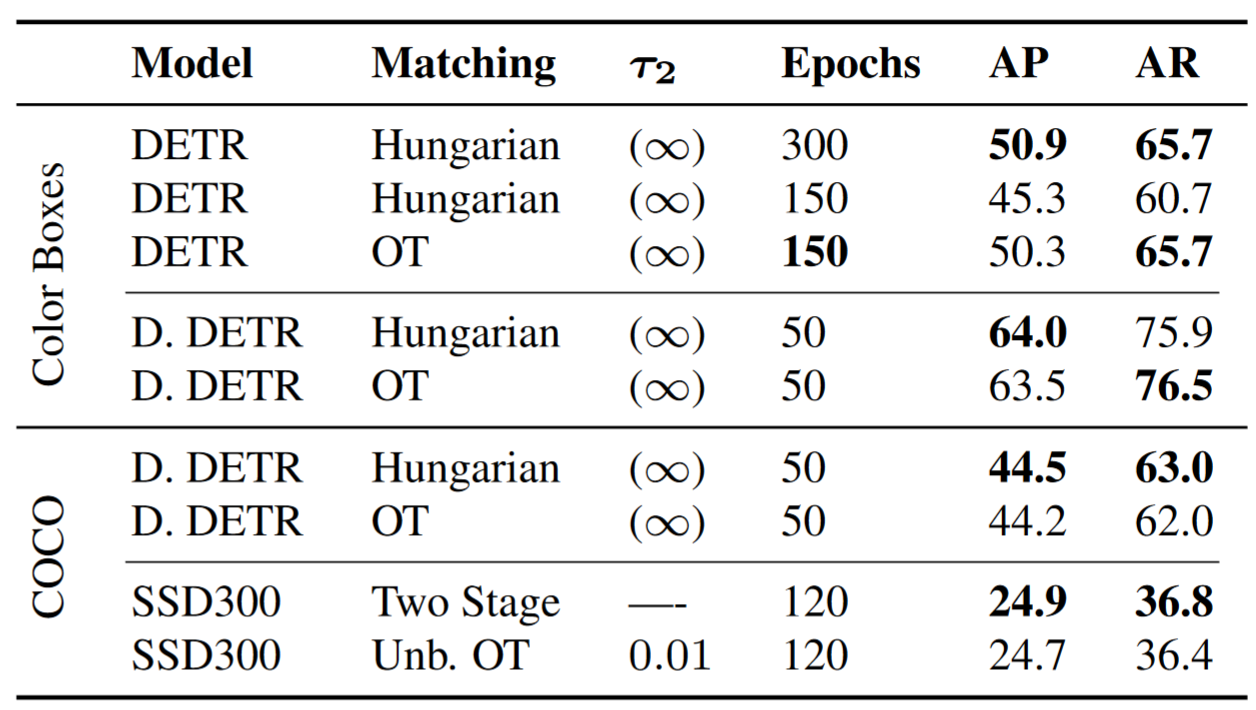
Results

Convergence curves for DETR on the Color Boxes dataset

Thank you !

hdeplaen.github.io/uotod/